Abstract.
The article shows that the depletion of existing oil and gas fields leads to the transfer of the main hydrocarbons production to the Arctic zone of the Globe, where their significant reserves are concentrated. It is stated that the management of geodynamic risks in the territories of oil and gas basins is associated with the use of mathematical modeling methods. Models for assessing geodynamic risks are divided into deterministic, probabilistic, and based on the use of the mathematical apparatus of fuzzy sets. To solve the problem of risk classification of the Arctic zone territories in relation to the location of oil and gas facilities, fuzzy models were used. The method of solving problems of managing geodynamic risks in the territories containing oil and gas complexes allows you to rank objects according to the degree of vulnerability in relation to the manifestation of geodynamic hazards. It is concluded that this approach makes it possible to justify high-quality management decisions in ensuring the safety of oil and gas complexes.
Keywords: oil and gas industry, geodynamic risk, territory, modeling, assessment, fuzzy model, hazard minimization.
Введение
Задачи оценки рисков на территориях с нефтегазовыми комплексами (НГК) приобретают особую значимость и всё большую актуальность в связи с тем, что количество аварий и катастроф здесь, связанных с природно-техногенными процессами геодинамического происхождения, продолжает оставаться высоким.
Приближающееся истощение существующих месторождений нефти и газа в регионах мира, находящихся в относительно благоприятных по климатическим, экономическим и экологическим условиям, приведет к переносу основной добычи туда, где ресурсы еще не разведаны или не разработаны.
Учитывая возникшие проблемы с поиском альтернативных видов топлива и источников энергии, в вопросах поддержания спроса на углеводороды и их добычи со всей очевидностью особую роль начинает играть Арктическая зона Земного шара, где сосредоточены их значительные запасы. По самым приблизительным оценкам в Арктике находится около 85 млрд баррелей нефти и столько же триллионов кубометров природного газа. При этом в российских границах сосредоточено около двух третей запасов газа и более 40% – черного золота [1].
И именно в Арктической зоне наиболее отчетливо проявляются специфические геодинамические угрозы, представляющие существенную опасность для создания, функционирования и развития нефтегазовых комплексов (НГК), на территориях, характеризующихся неустойчивой геодинамикой. Это – землетрясения, криповые подвижки, карстово-деформационные процессы, оползни, провалы, проседания и другие феномены, связанные с геодеформационными процессами в литосфере.
Воспроизвести геодинамические риски весьма проблематично натурно, в то же время их математическое моделирование имеет в современных условиях хорошие перспективы при решении задач обеспечения безопасного функционирования и развития нефтегазового сектора топливно-энергетического комплекса (ТЭК) России.
К настоящему времени разработан достаточно широкий спектр математических моделей, методов, алгоритмов и программных средств, позволяющих решать различные задачи оценки геодинамического риска на различных по геологическому строению территориях [2-6], в строительстве [7, 8]. В ряде работ затронуты вопросы управления геодинамическими рисками [9, 10]. В то же время, представленные математические модели, методы и алгоритмы не позволяют в полной мере решать такие задачи, как, например, оценка риска повреждения или разрушения промысловых и иных промышленно-хозяйственных объектов НГК, сетей инженерных и транспортных коммуникаций, относящихся к инфраструктуре НГК, оценка риска принятия неверного решения при разведке нефти и газа, а также оптимального размещения объектов НГК с учетом геодинамических рисков.
Всё вышесказанное требует разработки более совершенных математических моделей, методов, алгоритмов для решения указанных задач, а также программных средств их реализации.
Настоящая статья посвящена решению актуальной научной задачи – разработке современных математических моделей и алгоритмов оценки геодинамических рисков с целью обеспечения безопасности объектов НГК от возможных проявлений геодинамических угроз.
Модели оценки геодинамических рисков
При управлении рисками геодинамического характера на территориях НГК возникают четыре основные задачи: оценка безопасности территории, оценка состояния геологической среды, риск-классификация состояния объектов и их мониторинг. Все перечисленные задачи тесно связаны между собой, требуя для своего решения использование методов математического моделирования.
Модели оценки геодинамических рисков подразделяются на детерминированные, вероятностные и модели, основанные на использовании математического аппарата нечётких множеств [11].
Применяются детерминированные модели двух типов: двумерные и трёхмерные. Наиболее эффективны трёхмерные модели, базирующиеся на следующих граничных условиях:
(1)
где 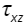 – касательные напряжения в плоскости XZ;
– касательные напряжения в плоскости XZ; 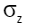 – вертикальная составляющая нормальных напряжений;
– вертикальная составляющая нормальных напряжений; 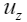 – вертикальная составляющая полного вектора смещений в геологической среде; P(x,y) – величина распределенной нагрузки в точке с координатами (x,y); ρ − средняя плотность вещества геологической среды,
– вертикальная составляющая полного вектора смещений в геологической среде; P(x,y) – величина распределенной нагрузки в точке с координатами (x,y); ρ − средняя плотность вещества геологической среды, 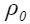 − средняя плотность вещества ниже условной модельной границы приложения внешней распределенной нагрузки;
− средняя плотность вещества ниже условной модельной границы приложения внешней распределенной нагрузки; 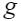 – ускорение силы тяжести; hmax – наибольшая величина отклонения модельной нижней границы от нулевого уровня; h – средняя толщина рассматриваемого модельного упругого пространства.
– ускорение силы тяжести; hmax – наибольшая величина отклонения модельной нижней границы от нулевого уровня; h – средняя толщина рассматриваемого модельного упругого пространства.
Детерминированные модели ориентированы на оценку геодинамических рисков для достаточно протяжённых территорий регионального масштаба. Однако они не всегда корректно “работают” на меньших по площади территориях вследствие разреженности данных о полях геодинамических аномалий.
Подобных недостатков лишены вероятностные модели оценки сейсмического риска. Предполагается, что последовательность геодинамических состояний геологической среды некоторой территории представляет собой простейший поток однородных событий, удовлетворяющий условиям независимости, однородности и ординарности.
Используя дифференциальные уравнения Колмогорова, описана динамика вероятностей pk(t) трёх состояний:
(2)
Состояния геологической среды определяются следующим образом. Предполагается, что в некоторый момент времени t0 геосреда обладает некоторым энергетическим параметром E0, отражающим опасные геологические процессы (ОГП).
Тогда состоянием 1 назовем такое состояние геосреды, при котором , т.е. она находится в равновесном устойчивом состоянии (E1 – энергетический параметр ОГП в момент времени t1).
Состоянием 2 назовем состояние, при котором геосреда находится в неустойчивом неравновесном состоянии, т.е. (E2 – энергетический параметр ОГП в момент времени t2).
Состоянием 3 назовем квазиравновесное состояние, при котором геосреда , причем
(E3 – энергетический параметр ОГП в момент времени t3).
Величины (i,j=1, 2, 3) физически представляют собой сумму энергетических параметров процессов, протекающих в геосреде, окончание которых приводит к ее переходу из состояния i в состояние j.
Однако к территориям, значительно неоднородным в тектоническом отношении, как это имеет место в Арктической зоне, применение и детерминированных, и вероятностных моделей также не всегда оправдано по причине неопределенности данных. Это, в частности, относится к решению задачи риск-классификации территорий Арктической зоны применительно к размещению объектов НГК. Поэтому для её решения осуществлено применение моделей, основанных на математическом аппарате нечётких множеств.
При формировании базы правил системы нечёткого вывода в качестве входных переменных использовались характеристики геосреды, полученные на основании анализа макросейсмических и других данных по геодинамическим явлениям, так и информация о напряжениях и смещениях, рассчитанных с помощью детерминированных и вероятностных математических моделей.
Оценка рисков на территориях Арктической зоны
Рассмотрим метод формализации взаимодействия природных, техногенных и антропогенных процессов в НГК. С этой целью определим множества X, Y, Z, отражающие совокупности факторов, способов и объектов природной, техногенной и антропогенной составляющих нефтегазового комплекса.
Элементами множества X (факторы воздействия на объекты НГК) определим следующие: x1 – «землетрясения»; x2 – «вертикальные и горизонтальные смещения на дневной поверхности»; x3 – «криповые подвижки»; x4 – «карстово-деформационные процессы»; x5 – «неоднородности геологической среды»; x6 – «неоднородности ландшафта»; x7 – «статическая нагрузка от зданий и сооружений»; x8 – «тектонические разломные нарушения»; x9 – «природные физические поля»; x10 – «технические воздействия»; x11 – «гидрологическая и гидрогеологическая сети»; x12 – «атмосферное влияние»; x13 – «организационно-правовое поле»; x14 – «социокультурное поле».
Элементами множества Y (способы воздействия на объекты НГК) являются: y1 – «механические колебания»; y2 – «геодинамические напряжения и деформации»; y3 – «опускания и поднятия»; y4 – «оползни»; y5 – «микросмещения по бортам разломов»; y6 – «подтопления, заболачивания»; y7 – «провалы»; y8 – «электромагнитные волны»; y9 – «акустические волны»; y10 – «температурное поле»; y11 – «инфразвуковое давление»; y12 – «трещиноватость геологической среды»; y13 – «поле биоактивного диапазона»; y14 – «пейзажное разнообразие»; y15 – «нормативные документы»; y16 – «общественное мнение»; y17 – «средства массовой информации»; y18 – «реклама».
К элементам множества Z (объекты НГК) отнесём следующие: z1 – «жилой дом, гостиница, общежитие»; z2 – «предприятие торгово-бытовой сферы»; z3 – «медицинское учреждение»; z4 – «управляющий комплекс»; z5 – «административное здание»; z6 – «общая насосная станция»; z7 – «складское помещение (склад, ангар)»; z8 – «энергетическая станция»; z9 – «кустовая насосная станция»; z10 – «транспортные магистрали»; z11 – «инженерные сети и коммуникации»; z12 – «трубопровод»; z13 – «геологическая среда»; z14 – «природный ландшафт».
Решим задачу оценки воздействия элементов множества X на элементы множества Z. Из экспертных источников применительно к конкретному территориальному полигону в Арктической зоне РФ, содержащему НГК, получены оценки степени воздействия элементов множества X через элементы множества Y (нечёткое отношение P на множествах X и Y), а также степени воздействия элементов множества Y на элементы множества Z (нечёткое отношение Q на множествах Y и Z). Матрицы нечётких отношений представлены в виде значений функций принадлежности и
; максимальные степени воздействия соответствуют единице.
Воздействие факторов через различные способы формально определяется в виде бинарного нечёткого отношения , заданного на декартовом произведении множеств
, а воздействие способов на объекты НГК формально определяется в виде бинарного нечёткого отношения
, заданного на декартовом произведении множеств
.
Определим композицию бинарных нечётких отношений , функция принадлежности которой описывается следующим выражением [11]:
,
(3)
В подобной интерпретации функции принадлежности нечёткого отношения отражают собой степень принадлежности множеству
значений воздействий внешних природных, техногенных и антропогенных факторов на объекты НГК. По существу, величины ri представляют значения риска для каждого из объектов НГК от конкретного природного, техногенного или антропогенного источника воздействия.
На рисунках 1 и 2 в убывающем порядке приведены интегральные риски для объектов НГК и интегральные риски от природных, техногенных и антропогенных процессов, соответственно.
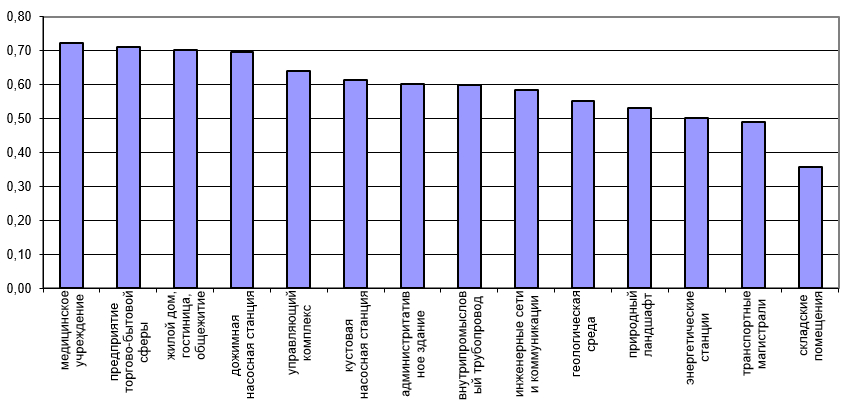
Рис. 1. Интегральный риск для объектов НГК
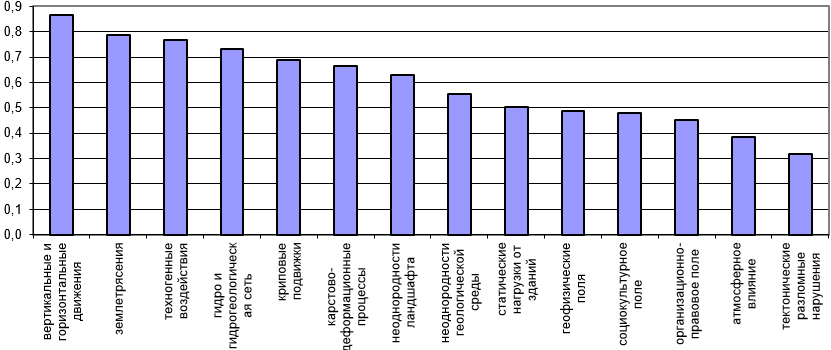
Рис. 2. Интегральный риск от природных, техногенных и антропогенных процессов
Как видно из рис. 1, наибольшему риску подвержены медицинские учреждения, предприятия торгово-бытовой сферы и жилые здания (0.7 и более), наименьшему – энергетические станции, транспортные магистрали и складские помещения (0.5 и менее).
Из рис. 2 следует, что наиболее опасными для объектов НГК являются вертикальные и горизонтальные движения на поверхности, землетрясения, техногенные воздействия, гидро- и гидрогеологическая сеть (более 0.7), наименее опасными – атмосферное влияние и тектонические разломные нарушения геологической среды (менее 0.4).
Предложенный метод формализованного представления рисков геодинамического происхождения для объектов НГК, основанный на нечётких отношениях, позволяет оценить объекты НГК на предмет их рисковой устойчивости, ранжировать природные, техногенные и антропогенные процессы по степени их воздействия на конкретные объекты, а также оценить интегральные риски для них и интегральные риски от указанных процессов.
Риск-классификация территорий и объектов Арктической зоны
Оценка риска принятия неверного решения по территориальному размещению объектов НГК, возникающего в случае отсутствия учёта пространственного распределения зон геодинамических аномалий и зон возможного развития опасных процессов геодинамического происхождения, является одной из важнейших задач оценивания безопасности в Арктической зоне.
Одним из важных этапов оценки рисков на территории НГК является ранжирование её различных зон по уровню безопасности объектов. Оно позволяют оценивать не только интегральный риск для всей территории, но и выполнять «точечно-площадные» оценки. Однако для их использования необходимо обладать достоверной информацией о достаточно большой совокупности характеристик, описывающих исследуемую территорию. Например, о гравитационных, магнитных, тепловых, техногенных и других полях, являющихся пространственно распределёнными. Следует также иметь четкое представление о неоднородностях геологической среды, наличии разломов, трещиноватости, знать о состоянии различных строительных сооружений, инженерных сетей, коммуникаций и других объектов НГК, информация о которых, как правило, представляется в виде экспертных оценок.
Поэтому актуальна разработка метода, позволяющего и надежно классифицировать объекты НГК, и выполнять их риск-анализ. Рассмотрим суть предлагаемого метода.
Разобьем некоторую исследуемую территорию на множество таксонов-участков . Во множество признаков, характеризующих риск-состояние каждого элемента T, учтён комплекс природных, техногенных и антропогенных воздействий, проявляющихся в пределах каждого таксона.
Комплексные параметры определены следующим образом:
p1 – «природные геологические процессы» (ПГП);
p2 – «особенности ландшафтно-геологического воздействия» (ОЛГВ);
p3 – «природные физические поля» (ПФП);
p4 – «техногенное воздействие» (ТВ);
p5 – «антропогенное воздействие» (АВ).
Параметр p1 отражает подмножество множества X, определенного выше, характеризуя: x1 – «землетрясения»; x2 – «вертикальные и горизонтальные движения на поверхности»; x3 – «криповые подвижки»; x4 – «карстово-деформационные процессы».
Параметр p2 включает подмножество, включающее показатели: x5 – «неоднородность геологической среды»; x6 – «неоднородность ландшафта»; x8 – «тектонические разломные нарушения»; x11 – «гидро- и гидрогеологические сети».
Параметр p3 – объединяет подмножество, характеризующих: x9 – «природные физические поля»; x12 – «атмосферное влияние».
Параметр p4 характеризует подмножество показателей, отражающих: x7 – «статические нагрузки»; x10 – «технические воздействия». Кроме того, дополнительно учитываются такие показатели, как техническое состояние объектов, загрязнение воздуха и влияние автомобильного транспорта.
Параметр p5 группирует показатели подмножества, относящиеся к полям гуманитарного характера: x13 – «организационно-правовому полю»; x14 – «социокультурному полю».
Каждый из таксонов-участков отнесён к одному из следующих классов: q1 – «безопасный таксон» (риск ); q2 – «слабо опасный таксон» (
); q3 – «умеренно опасный таксон» (
); q4 – «опасный таксон» (
); q5 – «значительно опасный таксон» (
); q6 – «чрезвычайно опасный таксон» (
); q7 – «катастрофически опасный таксон» (
).
Итак, общая задача заключается в том, чтобы классифицировать таксоны-участки, на которые разбивается исследуемая территория, содержащая НГК, по уровням безопасности (или уровням риска) при учете воздействий на них, исходящих от природной, техногенной и антропогенной составляющих окружающей среды.
Рассмотрим более подробно, как осуществляются процедуры оценки комплексных параметров pi (). В настоящей статье сделаем это на примере комплексного параметра p4 – «техногенное воздействие».
При кластеризации находящихся на территории объектов по техногенным воздействиям на их риск-состояние используем оценки статической нагрузки на приповерхностные грунты и технические воздействия, количественно определяемые через такие элементы множества Y (способы воздействия на объекты НГК), как: y1 – «механические вибрации»; y8 – «электромагнитные волны»; y9 – «акустические волны»; y10 – «температурное поле»; y11 – «инфразвуковое давление», а также данные по техническому состоянию объектов, загрязнению воздуха и влиянию автотранспорта.
Указанные способы воздействия на объекты НГК необходимо учитывать во всем их многообразии. Например, вибрации порождаются не только природными явлениями (землетрясениями, провалами, оседаниями), но и техногенными процессами (работой различных технических устройств, оборудования предприятий, движением транспорта). Это в полной мере относится и к другим способах воздействия: электромагнитные волны; акустические волны; температурное поле; инфразвуковое давление.
При этом величины влияний техногенных воздействий объектов на риск-состояние таксона-участка будем обозначать как (где i – порядковый номер влияния, k – порядковый номер объекта).
Определим признаки (верхний индекс указывает на вид влияния, нижний – на номер признака):
– «статическая нагрузка»;
– «вибрация»;
– «электромагнитное излучение»;
– «акустический шум»;
– «тепловое поле»;
– «радиационное излучение»;
– «инфразвуковое давление»;
– «загрязнение воздуха».
Признаки (
) определяются и обобщаются экспертами по данным наблюдений и приборных исследований, а затем оцениваются по 100-балльной шкале.
Опыт показал, что из-за совместного использования весьма разнородной информации для единообразия подхода к ее обработке, множество исследуемых объектов целесообразно ограничить четырьмя кластерами.
Для технических воздействий кластеры объектов определим следующим образом (верхний индекс указывает на порядковый номер вида влияния, нижний – на номер кластера):
– «слабое воздействие» (
);
– «умеренное воздействие» (
);
– «значительное воздействие» (
);
– «сильное воздействие» (
).
В скобках в относительных единицах указаны диапазоны воздействий.
В результате для каждого объекта исследуемой территории получим функции, характеризующие степень его принадлежности тому или иному кластеру по техногенному воздействию.
Далее рассмотрим классификацию объектов исследуемой территории по их техническому состоянию. Определим признаки технического состояния объектов:
– «состояние фундамента»;
– «состояние стен»;
– «состояние межэтажных перекрытий»;
– «состояние крыши»;
– «состояние окон»;
– «состояние систем коммуникаций».
Признаки (
) также определяются и обобщаются экспертами по данным наблюдений и приборных исследований, а затем оцениваются также по 100-балльной шкале.
Кластеры определим следующим образом:
– «ветхие здания, не подлежащие восстановлению» (
);
– «здания, требующие капитального ремонта» (
);
– «здания, требующие текущего ремонта» (
)
– «здания, находящиеся в хорошем состоянии» (
).
Как итог, получим функции принадлежности для объектов исследуемой территории, характеризующие их рисковое состояние в техническом отношении.
Наконец, определим признаки влияния автотранспорта на риск-состояние таксона-участка:
– «вибрации»;
– «электромагнитное излучение»;
– «акустические шумы»;
– «тепловое поле»;
– «инфразвуковое давление»;
– «загрязнение воздуха».
Кластеры определяются таким же образом, как и кластеры
.
Далее предположим, что значения влияний (где i – порядковый номер влияния, k – порядковый номер объекта) объектов на риск-состояние отдельного таксона-участка в пределах каждого из кластеров
(
;
) распределены по нормальному закону. При этом в качестве математических ожиданий
выступают центры кластеров. Также будем полагать, что радиусы
всех кластеров одинаковы.
Далее процедура выполняется в следующей последовательности.
Находим условные координаты каждого объекта (k – порядковый номер объекта) в кластерном пространстве:
, (4)
где – функции принадлежности для k-го объекта; m – количество кластеров (в нашем случае m = 4).
Затем определяем минимальное отклонение для k-го объекта в кластерном пространстве от центров кластеров:
;
, (5)
что позволяет определить, какому кластеру принадлежит рассматриваемый объект, и задать функции принадлежности для k-го объекта конкретному кластеру. по следующим правилам:
Правило 1: «Если , то
»;
Правило 2: «Если , то
»; (6)
Правило 3: «Если , то
».
Затем находим интегральный риск для каждого объекта по его техногенному влиянию на риск-состояние отдельного таксона-участка :
. (7)
Подобным образом оцениваются интегральный риск от технического состояния объекта и интегральный риск от влияния автотранспорта
.
Суммируя с определенными весовыми коэффициентами интегральные значения всех влияний на риск-состояние таксона-участка, оценим величину техногенного воздействия p4 для каждого k-го объекта в относительных единицах:
. (8)
Расчёты для всех остальных параметров (p1, p2, p3, p5), определённых выше, выполняются аналогичным образом. Затем выполняется интегральная оценка всей территории и проводится классификация её таксонов-участков по уровню их безопасности.
В итоге блочная риск-классификация территорий, содержащих НГК, основанная на нечёткой кластеризации, дает возможность выполнять их количественный риск-анализ, что важно при разработке стратегии управления территориальными системами, а также при их освоении и преобразовании.
Размещение объектов НГК с учётом геодинамических рисков
Рассмотрим модель и алгоритм оптимального размещения объектов НГК с учётом геодинамических рисков, обусловленных воздействием комплекса факторов природного, техногенного и антропогенного происхождения, рассчитанных на основе метода блочной риск-классификации.
Предположим, что на территории НГК планируется размещение множества объектов , и для каждого из таксонов-участков, на которые разбита территория, известна величина его риск-состояния
(
).
Требуется:
1) определить, насколько целесообразно размещение объектов в пределах рассматриваемой территории с точки зрения их безопасности в отношении геодинамических рисков, обусловленных воздействием природными, техногенными и антропогенными факторами;
2) если объекты находятся на опасных участках, необходимо перепланировать их размещение с учетом минимизации геодинамических рисков.
Рассмотрим алгоритм решения этой задачи на примере конкретного объекта . Определим его положение на рассматриваемой территории как
, где
– условная долгота;
– условная широта. Координаты конкретного объекта обозначим как
, если он «точечный». В ином случае его координаты задаются в виде матрицы координат.
Упростим задачу, полагая, что объект является «точечным», располагающимся только на одном участке-таксоне. При этом определено риск-состояние таксона-участка, величина которого равна
для объекта
. Если величина риска
(
– величина допустимого риска; reasonable – «разумный»), то объект может оставаться на прежнем месте размещения, если
, то объект
перемещается в другую позицию на рассматриваемой территории. Учтем два обстоятельства:
на новом месте расположения объекта с координатами
должна быть обеспечена его максимальная безопасность;
перемещение необходимо производить таким образом, чтобы объект оказался бы на наименьшем расстоянии от предыдущего места расположения, т.е. должно быть выполнено условие минимизации пути перемещения:
(9)
где Lh – расстояние между первоначальным и последующим положениями объекта .
Сам же алгоритм перемещения единичного «точечного» объекта представляет собой последовательность следующих действий.
1. Выполняется оценка величин риск-состояний для каждого таксона-участка вдоль взаимно-перпендикулярных профилей, на которые разбивается исследуемая территория.
2. Осуществляется проверка уровня безопасности планируемого места расположения объекта с учетом выполнении второго условия (9). Если это условие выполняется, то объект остается на прежнем месте, если нет, то объект перемещается в другое место на территории.
3. Производится выбор безопасного с точки зрения риск-состояний таксона-участка для нового размещения объекта. Этап реализуется в виде следующей последовательности.
3.1. Из всех таксонов-участков выбирается такой таксон-участок , что выполняются условия
и
(где
– матрица таксонов-участков с допустимыми значениями риска).
3.2. Выполняется проверка занятости таксона-участка каким-либо другим объектом.
3.3. Также должна быть свободна от объектов и некоторая область вокруг выбранного таксона-участка. Если это условие не выполняется, то происходит возврат к п. 3.1 и выбирается следующий по возрастанию значения риска таксон-участок, и вновь последовательно выполняем п. 3.2 и п. 3.3 до тех пор, пока указанное условие не будет выполнено.
3.4. Формируется массив , в который включаются таксоны-участки, в которые могут быть перемещены объекты.
4. Выполняется анализ массива на предмет определения таксона-участка, находящегося на минимальном расстоянии от предыдущего места расположения объекта.
5. Формируется массив таксонов-участков , занятых перемещенными объектами, и массив их координат.
После исчерпания множества объектов работа алгоритма завершается, и данные записываются в выходной файл в виде координат новых мест размещения объектов, который затем графически представляется в виде карты-схемы, отражающей модель оптимального размещения объектов в НГК.
Выводы
Наблюдающееся истощение действующих месторождений нефти и газа в различных регионах мира, приводит к переносу основной добычи углеводородов туда, где ресурсы еще не разведаны или не разработаны. Поддержание спроса на углеводороды и их добычи особая роль отводится Арктической зоне Земного шара, где сосредоточены их значительные запасы.
Управление рисками геодинамического характера на территориях нефтегазовых комплексов связано с решением четырех основных задач: оценка состояния геологической среды, оценка безопасности территории, риск-классификация состояния объектов и их мониторинг. Перечисленные задачи тесно связаны между собой, требуя для своего решения использование методов математического моделирования.
К настоящему времени разработан широкий спектр математических моделей, методов, алгоритмов и программных средств, позволяющих решать различные задачи оценки геодинамического риска. Модели оценки геодинамических рисков подразделяются на детерминированные, вероятностные и модели, основанные на использовании математического аппарата нечётких множеств.
К территориям, значительно неоднородным в тектоническом отношении, как это имеет место в Арктической зоне, применение детерминированных и вероятностных моделей не всегда оправдано по причине неопределенности данных. Это относится к решению задачи риск-классификации территорий Арктической зоны применительно к размещению объектов нефтегазового комплекса. Для её решения целесообразно применение нечётких моделей.
При формировании базы правил нечёткого вывода в качестве входных переменных необходимо использовались характеристики геосреды, полученные на основании анализа макросейсмических и других данных по геодинамическим явлениям, а также информация о напряжениях и смещениях, рассчитанных с помощью детерминированных и вероятностных моделей.
Новые модель и алгоритм размещения объектов с учетом обеспечения необходимого уровня геодинамической безопасности дают необходимые практические результаты, отличающиеся эффективностью управления развитием территорий, содержащих нефтегазовые комплексы.
Метод решения задач управления геодинамическими рисками на территориях, содержащих нефтегазовые комплексы, позволяет выполнить ранжирование объектов на них по степени уязвимости по отношению к проявлению геодинамических опасностей, а также провести ранжирование самих геодинамических процессов по степени их опасности в пределах оцениваемой территории. Подобный подход даёт возможность принимать более качественные управленческие решения по сравнению с традиционными процедурами при обеспечении безопасности нефтегазовых комплексов.
Список литературы:
Lindholt L., Glomsrød S. / Center for International Climate and Environmental Research. Discussion Papers No. 645. URL: http://ideas.repec.org/s/ssb/dispap.html. Oslo: Statistics Norway, Research Department, 2011. (Дата обращения 7.03.2021).
Ананьин И.В., Фаддеев А.О. Численное моделирование напряженного состояния тектонических нарушений в земной коре Центральной части Восточно-Европейской платформы (на примере Московско-Рязано-Саратовского авлакогена) / Материалы Международной конференции «Геодинамика и геоэкология». Архангельск: Ин-т экологических проблем Севера УрО РАН, 1999. – С. 11-14.
Ананьин И.В., Фаддеев А.О., Сим Л.А. Тектонические напряжения в земной коре центральной части Восточно-Европейской платформы (по результатам математического моделирования и структурно-геоморфологическим данным) / В сб.: Проблемы сейсмичности Восточно-Европейской платформы. М.: Изд-во ОИФЗ РАН, 2000. – С. 3-18.
Минаев В.А., Фаддеев А.О. Оценки геоэкологических рисков. Моделирование безопасности туристско-рекреационных территорий. М.: Финансы и статистика, Изд. дом ИНФРА-М, 2009. – 370 с.
Абрамова А.В., Бондарь К.М., Данилов Р.М., Минаев В.А., Павлова С.А., Попов А.Н., Фаддеев А.О. Моделирование геодинамических рисков в чрезвычайных ситуациях: монография / Под ред. К.М. Бондаря, В.А. Минаева, А.О. Фаддеева. Хабаровск: ДВЮИ МВД России, 2014. – 124 с.
Абрамова А.В. Математические модели оценки геодинамического риска на территории Армении // Технологии техносферной безопасности: Интернет-журнал. 2014. Вып. 4 (56). Электронный ресурс: http://ipb.mos.ru/ttb/2014-4. (Дата обращения 7.03.2021).
Минаев В.А., Топольский Н.Г., Фаддеев А.О., Бондарь К.М., Мокшанцев А.В. Геодинамические риски и строительство. Математические модели. М.: Академия ГПС МЧС России, 2017. – 208 с.
Минаев В.А., Фаддеев А.О., Пылькин А.Н., Бондарь К.М., Кираковский В.В. Гибридная ANFIS-сеть как инструмент снижения рисков при разработке проектов застройки территории / Материалы XXIII международной научно-технической конференции «Системы безопасности – 2014». М.: Академия ГПС МЧС РФ, 2014. – С. 116-121.
Минаев В.А., Фаддеев А.О., Бондарь К.М., Сычев М.П., Видов С.В., Кираковский В.В., Кузьменко Н.А., Попов А.Н. Математическое моделирование геодинамических рисков: оценки и перспективы / Под ред. В.А. Минаева, А.О. Фаддеева, К.М. Бондаря. Хабаровск: Издательство Дальневосточного юридического института МВД России, 2015. – 212 с.
Минаев В.А., Фаддеев А.О., Кузьменко Н.А. Моделирование и оценка геодинамических рисков. М.: РТСофт – Космоскоп, 2017. – 256 с.
11. Ярушкина Н.Г. Основы теории нечетких и гибридных систем: Учебное пособие. М.: Финансы и статистика, 2004. – 320 с.
1. Lindholt L., Glomsrød S. / Center for International Climate and Environmental Research. Discussion Papers No. 645. URL: http://ideas.repec.org/s/ssb/dispap.html. Oslo: Statistics Norway, Research Department, 2011. (Accessed 7.03.2021).
2. Anan'in I. V., Faddeev A. O. Numerical Modeling of the Tectonic Disturbances Stress State in the Earth's Crust of the Central Part of the East European Platform (on the Example of the Moscow-Ryazan-Saratov Aulacogen) / Proceedings of the International Conference "Geodynamics and Geoecology". Arkhangelsk: Institute of Environmental Problems of the North of the Ural Branch of the Russian Academy of Sciences, 1999. – Pp. 11-14.
3. Anan'in I. V., Faddeev A. O., Sim L. A. Tectonic Stresses in the Earth's Crust of the Central Part of the East European Platform (Results of Mathematical Modeling and Structural and Geomorphological Data) / In the Сollection: Problems of Seismicity of the East European Platform. M.: Joint Institute of Earth Physics RAS Publishing House, 2000. - Pp. 3-18.
4. Minaev V. A., Faddeev A. O. Geoecological Risk Assessments. Modeling the Safety of Tourist and Recreational Territories. Moscow: Finance and Statistics, INFRA-M Publishing House, 2009. – 370 p.
5. Abramova A.V., Bondar K. M., Danilov R. M., Minaev V. A., Pavlova S. A., Popov A. N., Faddeev A. O. Modeling of Geodynamic Risks in Emergency Situations: Monography / Edited by K. M. Bondar, V. A. Minaev and A. O. Faddeev. Khabarovsk: Far Eastern Law Institute of the Ministry of Internal Affairs of Russia, 2014. - 124 p.
6. Abramova A.V. Mathematical Models of Geodynamic Risk Assessment on the Territory of Armenia. 2014. Issue 4 (56). URL: http://ipb.mos.ru/ttb/2014-4. (Accessed 7.03.2021).
7. Minaev V. A., Topolsky N. G., Faddeev A. O., Bondar K. M., Mokshantsev A.V. Geodynamic Risks and Construction. Mathematical Models. M.: Academy of the State Fire Service of the Ministry of Emergency Situations of Russia, 2017. – 208 p.
8. Minaev V. A., Faddeev A. O., Pyl’kin A. N., Bondar K. M., Kirakovsky V. V. Hybrid ANFIS-network as a Risk Reduction Tool in the Development of Territory Development Projects / Proceedings of the XXIII International Scientific and Technical Conference "Security Systems-2014". M.: Academy of the State Fire Service of the Ministry of Emergency Situations of Russia, 2014. – Pp. 116-121.
9. Minaev V. A., Faddeev A. O., Bondar K. M., Sychev M. P., Vidov S. V., Kirakovsky V. V., Kuzmenko N. A., Popov A. N. Mathematical Modeling of Geodynamic Risks: Estimates and Prospects / Edited by V. A. Minaev, A. O. Faddeev, K. M. Bondar. Khabarovsk: Publishing House of the Far Eastern Law Institute of the Ministry of Internal Affairs of Russia, 2015. – 212 p.
10. Minaev V. A., Faddeev A. O., Kuzmenko N. A. Modeling and Assessment of Geodynamic Risks. M.: RTSoft-Kosmoskop, 2017. – 256 p.
11. Yarushkina N. G. Fundamentals of the Theory of Fuzzy and Hybrid Systems: Textbook. M.: Finance and Statistics, 2004. – 320 p.
This is an open access article distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0)